Over the course of the past couple of days I've read your entire thread from start to finish. What a read! Incredible work developing the car, and I love the analytical process and write-ups throughout. I hope you enjoy your retirement and get to enjoy the car for years before it becomes time to stop autocrossing. I feel like it's well deserved!
Thanks guys. I have a lot of fun writing these things. I am glad someone finds them useful and/or entertaining.
No One is Laughing -
Tow Hitch
Over the last 40 years I have had trouble with my left knee (my old diaper changing injury – another story). The knee was finally replaced two years ago leaving me with some lack of flexibility during the recovery. Climbing up on the trailer to get Mistress on and off was getting to be a little tricky. I reasoned that a winch on the trailer would save me climbing up and down. It could also be useful if the car broke down at an event. I have a “come-along” but that is tedious for routine use.
I put a small winch on the trailer to pull the car up. Nothing special. It has long jumper cables that can be run directly to the truck battery as needed.
I needed a tow point on the car to attach to. As is my way with things - I made one. I wanted something unobtrusive, almost hidden. What I came up with was a simple ¼” rod bent in a “U” shape and welded to a bracket bolted to the front frame. I reasoned it did not need to be exceedingly strong since I was just pulling the car up a ramp. I calculated the maximum load it would see was about 2000 pounds based on the weight of the car and some geometry. It is not like we were pulling a wrecked car out of a ditch or something.
I was very wrong. The max load happens when lowering the car off the trailer. The car stops rolling for a moment, cable goes slack, car starts rolling, cable goes tight… Tow bracket snaps in half (ping!).
First event of the season and Mistress is rolling itself untethered off of the trailer towards someone’s pickup truck.
I leapt into action! On the second step I was realizing there was nothing I could do and that this was not going to end well. The third step was trying to regain my balance. The fourth step never happened.
They say you can tell how old you are by how much people laugh when you fall. Toddlers are a riot. In this case, no one was laughing. I landed on both extended arms which promptly collapsed and planted my face hard into the asphalt.
People came running. I could not move at first. Calls to 911 were in the works when I was able to struggle to my side and was helped to lean against the trailer. Somehow my arms and shoulders were not broken although they took quite a shock. Fingers not working at first. Face bleeding. Sunglasses mangled. Stunned but, somehow, I think I am alright… No 911 call.
As Mistress rolled off the trailer it turned itself and rolled harmlessly onto the grass.
After sitting there for a while answering questions about how many fingers were being displayed, I was helped to my feet, patched up, and proceeded on a slow and slightly wobbly course walk accompanied by a couple of friends would not let me out of their sight. I was never alone the rest of the day.
The reasoning was that, if I stayed at the event, we had several medical people in the club who could watch me. Better than loading up and having issues alone on a country road two hours from home. Made sense at the time but when I got home that evening my wife took one look at me (you idiot!) and drove me to emergency. No further issues found but I missed the next event and it took most of the summer to fully recover.
So… I needed a right and proper tow loop on the car. I bought a Competition Engineering C3435 from Summit. This is a robust 5/16” steel plate with a hinged burnout loop of the same material. You could probably pick up the car with this thing and shake it. Except, the car is made of sheet metal.
There is nothing robust on the front of the car except the bumper and I did not want to mount that high to work with the winch on the trailer. The winch is mounted fairly low and the angles would be all wrong for the last few feet. It is a short trailer.
The plan was to insert a heavy backing plate inside the radiator support frame for the tow loop to bolt into.
I started with a piece of 3/8” plate cut to match up with the tow loop.
This would be placed inside the radiator frame on the right side. There is a narrow opening on the frame at the bottom right corner where it could be inserted. But it has to be precisely placed and held in position to get the bolts into it. To allow this I used a 3/16” rod with a sharp bend in the end and tack welded it into a hole drilled into the corner of the plate.
Now I have a “handle” to insert the plate and hold it in position.
Using the tow loop as a template I drilled and tapped the backing plate.
This did not seem to have enough thread engagement to be utterly fail proof so I welded Grade 8 nuts to the plate after aligning them to the threads using dummy bolts. I know the temper on the nuts is gone but I now have over ½” thread engagement.
The angle of the radiator frame put front of the tow loop too high on the car behind the facia. It also hit the intercooler. I knew this would happen and had a plan for it.
A manual hydraulic press is one of those shop tools you wonder how you did without for all those years.
You have to be careful with these things. The forces can get extremely high. This tool can snap those Harbor Fright C clamps in an instant and imbed shrapnel where you don’t want it.
With my tow loop bent as needed I completed the assembly with 3/8” Grade 8 bolts. I cut the excess off of my “handle” on the backing plate leaving just a bit sticking out of the opening in the frame.
I may have to rework it if I put a splitter on the car but we will figure that out when the time comes. In the meantime, this thing would rip the car apart if enough force were applied. It is placed right where the winch needs it and is almost hidden. Should have done it up right in the first place.
Brake Line Replacement – Antilock Brakes
You may recall that when I installed the supercharger I was bitching about how the antilock brake module had to be relocated and that it left the brake lines in a tangled mess. I finally got into fixing it last spring in conjunction with the radiator replacement. The entire front of the car was opened up exposing all the plumbing. It seemed like a good time to make things right.
This was not without some trepidation. I have never worked on this part of the braking system before and the warnings of “only the dealer can properly bleed the antilock brakes” were not lost on me. The nearest Ford dealer is more than an hour away from here. But it needed to be done and: 1 – I figured I could figure it out. 2 – The local car shops are very good. 3 – You can actually buy electronic tools to do this now.
When it comes down to it: You need to fake out the control system to cycle the antilock valves while actually bleeding the brake line at the same moment. We got this. I started the job.
First thing – I made a chart of where all these lines went. You could theoretically do one line at a time but in reality, they are all bundled together and you have to take more than one off to get them past each other. Getting them crossed up would be a nightmare. Make a sketch.
It is ugly but it served the purpose. At first I was going to just splice in short bits around the antilock module. After messing around a bit I decided to replace everything on the front of the car. The lines that run to the rear wheels have splice joints in the front wheel wells.
Notice the fittings are “poka yoked” (error proofed) so they cannot be cross connected on the assembly floor.
I bought some copper nickel line (easier to bend) and a brake flaring tool from Summit. I immediately had trouble.
The tool would not make proper flares. I played around with-it making flares until I could mimic what was on the car using a large thick washer as part of the first step.
Turns out I had two problems: 1 - The dies on the tool for “Step 1” & “Step 2” were labeled backward. If you use them as labeled you get some of the weird flares shown below. 2 – Most of the flares on the car (but not all of them) are “bubble flares” not double flares. I was using the wrong tool.
The black piece above is an original from the car.
The flares I ended up with by using the tool backwards from its design and adding an extra step were actually double bubble flares. They had the exact shape of the original bubble flares but were actually folded over in two layers on the end of the bubble. I would say they are stronger than actual bubble flares. And they did not leak.
By the time I was finished with the project I had figured out the miss-labeled die issue and could also make proper double flares with the thing. This was good because Ford was not consistent. Some of the connections ARE double flares.
Worse than that, some of the fittings were English, some were metric, and on opposite ends of the same tube. EGAD! What were they doing over there at Ford?
I figured this out when some connections would just not fit up right. My new fittings from Autozone were not making up properly with some of the originals. Dangerously similar, but not exact. I finally took a caliper to some fittings and noted different measurements. Now I had something new to keep track of.
If you read about doing brake line work on these cars there are dire warnings about all this. Yup. It is true.
I finished all this work and then did an extensive brake bleed while cracking fittings along the way to get as much air out as possible. Then a leak check. This is when I found a couple of the English/metric fitting mismatches noted above.
To do the leak checks I put a couple of clamps on the brake peddle to hold it down for a couple of hours and then checked if it still had pressure and inspected for leaks.
I then had to put this on hold for a month while I did the radiator job. With the radiator installed it was time to finally do a proper antilock brake bleed job. At this point the brakes were very soft and spongy. The car was not drivable.
So – Air is trapped inside the antilock module behind the little valves that pulse the brakes when the tires skid. This is also part of the traction control system. There are four little valves, one for each wheel.
Some cars have little bleeders on the antilock module allowing you to manually bleed the unit. Some cars do it automatically. This car has none of that.
Without special equipment you have to find a way to make the control module think it is happily driving down the road while it has one or more wheels skidding as the brakes are applied. As the car tries to recover from the “skid” by pulsing the little valves you have to bleed the brakes.
Driving on ice with loose bleeders spewing brake fluid all over the streets comes to mind. Probably not a good idea.
Riding on a creeper cart under the car while bleeding the brakes? Hmm, Car is too low for that and death is all too likely.
Ahh – Once again having a midrange scissors lift comes in handy. And I have an old Harbor Freight diagnostic tool that can reset antilock faults (most diagnostic tools can’t do this). Speed bleeders (they have check valves in them so air can’t get back into the lines) come in handy also. In fact, they are necessary for doing this safely (see below).
Here is the set up: Remove one of the rear rotation sensors and let it dangle (now the controls think that wheel is not turning). Car is on the lift with all wheels removed. Engine running, in gear. It thinks it is going down the road at about 20 mph.
Open the bleeder on the wheel with the sensor removed. Have someone gently apply the brakes (my wife gave up a whole afternoon for this joyful exercise). The car will chatter the antilock valve for that wheel allowing the air bubbles through. Then shut down and bleed that line all the way back to the wheel (you have to purge the bubbles that were released). Put the rotation sensor back in position, and do the same for the other rear wheel.
So - All ya gotta do is reach into a spinning wheel well in an operating car... See some warnings below...
At each step in the process you have to reset the antilock module faults that will come up. Otherwise, the antilock system will stop working after the first attempt.
The front wheels are easier. They are never turning so you don’t have to mess with the sensors. Otherwise, same procedure, car is in gear, thinks it is going down the road, brakes applied as brake is bled. Then purge the bubbles out of that line and reset the faults.
I went through this entire process twice. Used about a gallon of brake fluid.
And it worked! Antilock brakes bled and were fine all summer. You don’t need a dealer or a shop. You just have to be innovative, patient, and stubborn.
SAFETY - The operating car in the air has risk but it has no wheels on it. Secured on four good jackstands on pavement it is not likely to fall and if it did it would not go far.
The risk is reaching past the spinning wheels. This is hazardous. Short sleeves, hair tied back, etc. are good ideas. Keep your wits about you and move deliberately. The moving wheels will not stop if you get caught in them. They won't even slow down a little.
In fact - The speed bleeders could be considered an important safety device here. You can open the speed bleeder, put the car in gear, pump the brakes and take the car back out of gear to close the bleeder. Otherwise your arm is in there working the wrench the entire time. Even at idle speeds the wheels will kill you if given a chance. Don't give them the chance.
You also need the proper diagnostic tool to reset the antilock faults.
This work was completed about a week before the first event. I was running out of time and not sure I would be successful. Even getting the car into a local shop was “iffy” because they all have a long backlog. Hate to admit it but, as insurance I bought a tool that can automatically bleed the antilock brakes on this car.
It is still in the box.
Pully Alignment Issues
Last season I had issues with the serpentine belt popping off in mid run. This happened several times wrecking the $25 belt and also wrecking the run. I started keeping two or three spares and changing them for every event.
On reflection this started happening after removing the AC compressor and replacing it with an idler. But at about the same time I also changed the power steering pulley to a larger diameter. This was to overdrive the pump and make the car easier to steer with all that caster dialed in to the front suspension. Something is not lined up with something else.
So - How accurately do these eight pulleys need to be aligned with each other?
We are dealing with a six-groove rubber belt stretching over eight pulleys. One of the pulleys is a spring tensioner that should take up any slack. Why does the belt come off in the first place?
Since this is an autocross car the engine RPM is constantly changing rapidly. That is the key. The centrifugal supercharger is also constantly changing load varying from perhaps 40 HP to near zero and back again. This means that the belt is constantly stretching and shrinking.
A hard gear change or touching the rev limiter jumps several hundred RPMs in an instant while putting enormous instantaneous load on the belt (and the valve train, and the drive train). A snapping rubber band moves quickly but still takes time to snap. The spring loaded take up pulley has inertia and also takes time to move. Not a lot of time, but it is not zero. Parts of the serpentine belt will go dead slack for a moment through these transitions.
Worse than that, the belt is whipping around the pulleys, and the centripetal force is trying to pull it away. It is being flung off with every curve.
So, the belt is entirely disengaged from at least some of the pulleys every time I shift gears and squawk the tires. As the belt wears and loses some of its integrity (stretches more) the same happens while spinning the wheels out of a corner.
The belt is “thrown” constantly from one pulley to the next. The pulleys have to be aligned well enough to “catch it” when it is thrown.
The six grooves on the belt are 4 mm apart. To catch the flying belt each pulley should be aligned within half that distance to the previous one. Or we could just say get them all within 2 mm of the crankshaft and be done with it. There is our target.
Two mm (0.08 inches) is not in the territory of laser alignment, dial indicators, or even calipers. You can see it and measure it with a good scale. But you need a good reference point and that would be a good straight edge.
What I used for a straight edge was aluminum tile edge trim. Most building supply stores have it in six-foot lengths. It is very light, easy to cut to length and, if it has not been beat up, very straight.
How straight? Checking a piece against the bathroom mirror – Very straight. I would say that it is withing a couple of thousandths. Good enough for this. And it comes in all sorts of designer colors! I chose black.
I made two pieces for short & long measurements.
The various pulleys all have different thicknesses on their edge flanges. Some are stamped steel, some phenolic, some machined aluminum. The cast aluminum harmonic balancer on the crankshaft has the thickest edge. With my short straight edge held against the flange of the harmonic balancer the belt measures 7 mm away.
Seven mm is the reference. In a perfect world the belt would measure 7 mm from the straight edge at the entry and exit from each pulley.
So here is the first round of measurements:
Pulley Gap (mm) Miss-alignment
Crank 7 0
Power Steering 8 1
Alternator 7 0
First Idler 5 -2
AC (New Idler) 3 -4
Supercharger 7 0
Tensioner 6 -1
Water Pump - -
And we have a winner! The new idler replacing the AC compressor is way out of whack. It was also not parallel to the overall plane of the other pulleys.
In the photo below you can see a gap between the straight edge and the pulley near the bottom. But the straight edge is touching it at the tip (where the white line is painted on).
Not only is this pulley out of place to catch the belt it is also throwing it crooked to the next pulley.
The misalignment was easily solved by adjusting the rear mounting bolt holding the pulley bracket.
I used some numbered drill bits as thickness gauges to guide me as to when the pulley was parallel to the straight edge (I don’t care what the gap is as long as it is the same in both places).
The drill bits are easier to use than feeler gauges in this situation. Keep adjusting until you can find a bit that is barely touching both sides of the pulley.
This got the pulley aligned but it needed to move about 3 mm towards the engine. I could not do this adjusting the bracket. It is doweled in place.
I had to adjust the bushing behind the pulley.
Neither my local hardware nor Amazon had a suitable part. I could either grind the bushing or adjust how the bearing is pressed into the phenolic pulley. I decided to use the press because if I went too far I could always push it back a little.
I did not have a die to match up with the outer race of the bearing. So, I made one from a strip of brass.
And carefully moved the bearing 3 mm in the pulley. Took two attempts.
Final measurement on the AC Idler pulley 6 mm for a difference of -1 mm. On target.
Note that in my measurement chart above the First Idler was at 5 mm for a difference of -2. This pulley works on the back side of the belt (no grooves) so it was just registering part of the offset of the AC Idler. With the AC Idler fixed the First Idler was spot on.
Also, I did not measure the water pump pulley because it also works on the back of the belt and is less than an inch from the crankshaft. It does whatever the crank shaft pulley does.
Errors in this measurement method could come if the surface of the harmonic balancer is not exactly perpendicular to the crankshaft (runout). I did not check for this (could put a dial indicator on it and bar over the engine to see how the reading changes). I expect it to be minimal since this is a machined surface on a major rotating part.
So here is to a new season and running all through it with the same belt (fingers crossed).
Updating the Rear Suspension - Now With Much More Madness!
Back in 2015 I revised the rear suspension on Mistress from the OEM triangulated four link to a parallel five link.
The four-link design has some advantages (no Panhard required) and is often used by rock crawlers for a variety of reasons. But for an autocrosser it did not seem appropriate at the time.
My opinion has not changed: With the four link the two upper links swing on different arcs from each other and from the lower links. Therefore, the bushings need to be fairly soft to prevent the suspension from binding. Most aftermarket suppliers have found the sweet spot for the bushings between good control and binding. With the soft OEM rubber I could feel the axle steering itself. On videos I could watch it moving laterally almost two inches. Not acceptable. On page two of this log I switched it to a five-link based loosely on the Steeda rear suspension kit.
But there were two problems: 1 – I already had an excellent MM Panhard on the car and it is not compatible with the Steeda geometry. 2 – I did not have a team of suspension engineers from Steeda or MM to help work out the details. And, as it turns out, that is where the devil is.
The resulting custom rear suspension was light years ahead of the OEM design. The car was much more predictable and planted. However, compromises were made and my final geometry was sub-optimal. I knew this at the time but was happy with it until the supercharger came along.
My name is not Earnhardt, Petty or Andretti but I can tell that with the additional power the car easily gets loose in the rear (no surprise there). The problem was that it was inconsistent about it. Mapping the suspension and running the numbers through a spreadsheet has provided the answer (Ah yes… There’s your problem…)
So after ten years and an additional 200 HP. It was time for an upgrade. For reference, here is the 2015 configuration:
If you compare the photo above to a Steeda kit (or the photo below) you will note that the white upper link towers should be leaning way back and longer. But this could not be done because of the cross bracing on the MM Panhard. So, I shortened the towers and tilted them up to make everything fit.
This dramatically increases a calculated value called “anti-squat”. Anti-squat affects how the car puts power down and its stability powering out of corners. Not a big deal on a 200 HP car. It is a very big deal on a 400 HP car. More on that later.
THE PLAN
1 – Map the rear geometry of the car. Locate all the linkage connection points and calculate roll centers and anti-squat. This job is much easier today with a LASER level. I mapped the front also for the record but planned no changes at this time. The front is a full MM design (even the K-Member) and the geometry is about as optimized as you can make a McPherson Strut suspension.
2 – Revise the MM Panhard bar bracing without weakening it to make way for better geometry as calculated above.
3 – Install new linkage geometry for the upper arms to fix the above issues.
4- Replace the OEM lower arms (finally!). All connections points to be solid spherical rod ends (no urethane).
5 – And then the MADNESS! While the axle is out of the car: Cut and weld it to negative one degree camber on both sides. My retirement/birthday present last fall was a new welder with this in mind. This is kind of radical. Most people don’t do this. Look closely at the rear tire in the photo below (Bwaa Haaa Haaa Haaaaaa!).
These changes have been made. These deeds are done. Mistress has been out for a couple of quick test drives. She tracks straight and nothing flew apart. The ride is not as harsh as I imagined but it was already to the point where long trips are brutal and require earplugs.
The first event is in two weeks and should be an interesting shake-out. Hopefully it will not be a “Egads - What the hell have I done to this car!” situation. Wish me luck.
My spirit guide for this has been a book by William R. Mathis: Mustang Performance Handbook Vol. 2. I have lots of books on making your car handle and Mustang performance. However, if you have a Fox Body or SN95 car – This is required reading. It is an investment. It is full of specific highly detailed advice. It includes fabrication diagrams for every modification. It covers specific mods needed for autocross, road track, and drag racing. Got mine on Ebay for $80.
This is a lot to process and download so the write up will probably be in at least five or six parts. The season begins soon - Let’s Go Autocrossing!!
More to come.
Hell yes, more details needed on the rear camber process. I have read the method using a torch to heat shrink the top surface (in Herb Adams book), but I am not familiar with the cut and weld method.
Once again another great detailed post. I searched Amazon for that book and the cheapest one is $133. Being I can not autocross any more, I'll pass on this purchase.
Also, I believe there was a big CAM autocross lat year in Grissom Indiana. Are they holding one this year?
Keep up the excellent posts.
In reply to Shavarsh :
I have the Herb Adams book: Chassis Engineering. It is an excellent guide on how to build a race car. The book I mentioned above is just as detailed and is written specific to Fox Body (and by extension SN95) cars.
Both books talk through adding a maximum of -1 degree of camber to a solid rear axle by heating/bending (Adams) or cutting/welding (Mathis). Neither goes into great detail on how to proceed but both admonish that one degree is the mechanical limit. Mathis notes that more than one degree would also start to diminish acceleration and braking.
I opted for cutting/welding because that seemed more exact than heating and bending. More control of the process is desirable. However, in practice, the steel moves when you heat it either way. I found that after cooling my work added another 0.2 degrees more more on its own.
I had to recut/reweld one side because it went too far. With the heating/bending method you should also be able to make secondary adjustments if needed.
My method was to cut almost all the way through to use the bottom remainder of the tube as a hinge. This helped keep alignment and length intact. However, it also meant I was welding more on the top than on the bottom. On cooling, the steel moves on its own
I also found that the -1 degree limit is really an approximation (your mileage may vary). Most people are not modifying a Ford 7.5" housing, Moser 27 spline axles with an Eaton Tru-Trak. I had binding at the splines and had to grind out the outer bore of the Tru-Trak on both sides. It is a weird car...
I will be detailing all of these shenanigans with photos in upcoming articles. The madness continues.
In reply to Mustang50 :
Hi Mustang50. Thanks for the comment. Yes the CAM Challenge series at Grissom in Peru, IN on the weekend of Aug. 8, 9, 10 this year. I am considering going although it conflicts with a local points event. Have not been to it in a few years. CAM cars are very entertaining to watch and even more entertaining to drive.
In reply to KentF :
Great to hear from you again. Hope you're having a nice Easter!
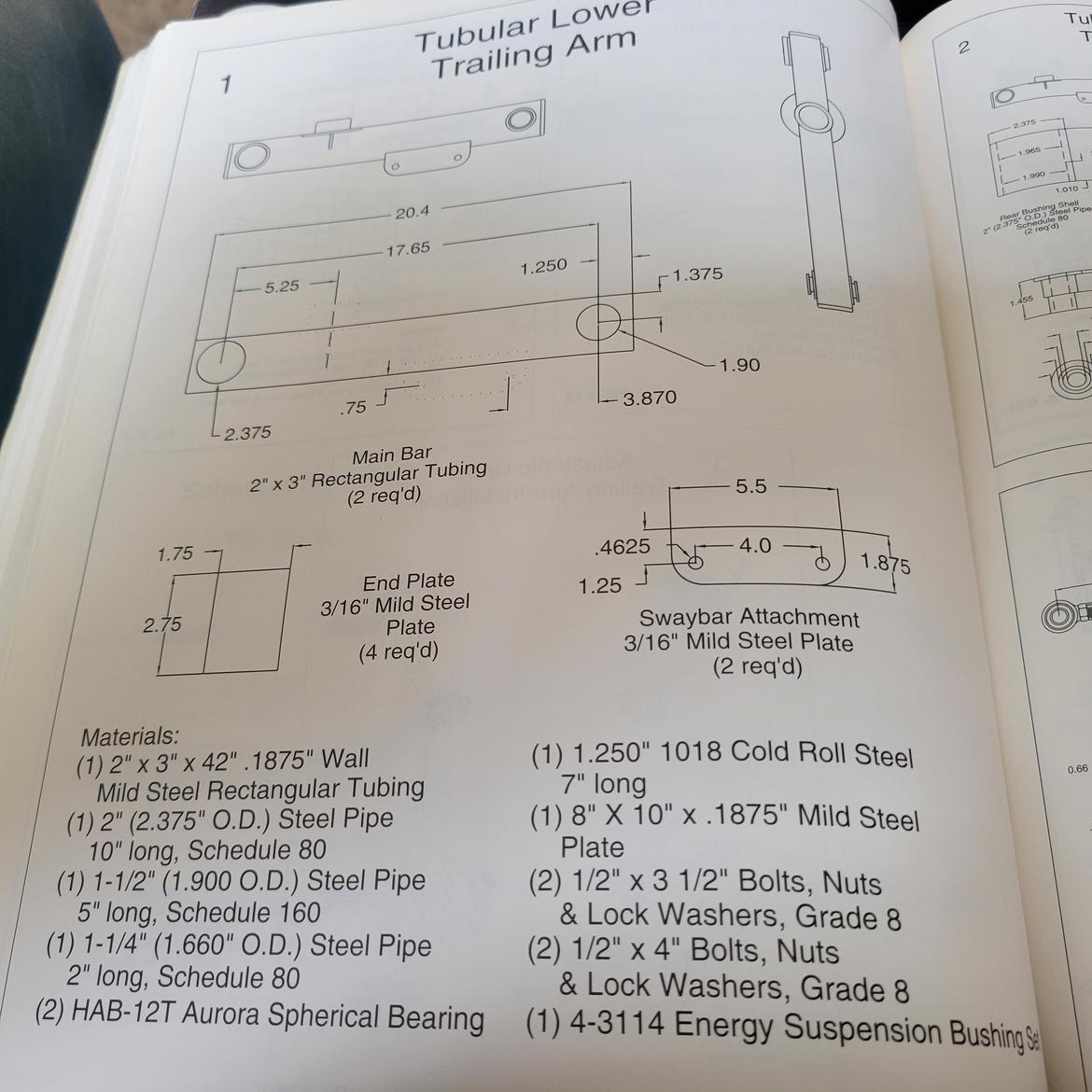
Mapping The Car – Anti-Squat
If you want to get somewhere it helps to know where you are starting from. Even if you are not sure where you want to go.
Back in 2015 I reworked the OEM rear suspension to something based on the Steeda Kit for this car. “Something based” are the operative words. Designed from photos online and some engineering knowledge. I think I was on a good track until I was assembling the thing and realized the upper towers would not fit with the MM panhard.
The Steeda panhard is simpler than the MM because it is intended to be welded in and has no cross bracing from one side to the other. I expect they intend for you to add cross bracing elsewhere. It is a nice clean design.
The MM panhard is intended to be bolted to the frame (you can also weld if for greater strength). It has two tubes running behind the attachment points that tie one side of the frame to the other. Loads are distributed into both sides of the car. Very strong, perhaps a little heavier (my guess). It is a bulletproof design.
I was not willing to start butchering the panhard framing so I basterdized the design by tipping the upper towers forward, shortened them, and shortened the upper links.
I did not know where I was so I did not know where I was going. Even so, I ended up in a better place (wherever it was) and the car handled better. Something about blind squirrels and nuts comes to mind.
Ten years and an additional 200 HP later I am now willing to basterdize the MM panhard and create something more/better based on the Steeda design. And this time I will know where I am starting from.
First step; buy a LASER level. You can have a reasonable one now for about $35.
These things are self-leveling and put out a bright LASER cross hair to use as a reference.
Second, get the car safely in the air and level on its suspension as if it were sitting on perfectly level ground. This is fussy and iterative and took about two days work even with a lift.
The front was sitting on the support frames and alignment stands I made some years ago. The axle was on the shortened HF stands also from some years ago. Car is supported on its suspension and dead level (as measured from the wheel centers to the laser beam). In my case I was able to set the LASER exactly at the elevation the ground would be including tire deflection. If the exact elevation can’t be set then you can just do math and add or subtract the difference.
I found the actual centerline of the car in a couple of steps:
At the rear I used a length of wood quarter round poked through the suspension. Marked it at the rotors. Took it out, measured and marked the midpoint, put it back and hung a plumb bob. Photo below shows the string tied to a magnet as an example.
I did a similar operation at the front but since it was on the alignment stands I used the two tape measures that are for measuring tow in.
Once the center was found I marked it on the bottom of the car in a few places so the vertical laser line could be set on it.
Look closely and you can see the green laser on the paint mark at the K-member running all the way to the cross hair on the garage door.
Other general measurements needed are the exact wheelbase of the car. Tire rolling radius (with deflection), vehicle CG height, vehicle mass (with driver), Front and rear suspension un-sprung mass.
Vehicle CG height I used from my books for this car at 16”. I have the steel to fabricate some corner scales which will give me the actual CG but was sick last winter and did not get to them. That project will come after this season.
The vehicle weight I have from earlier readings on a commercial scale (truck stop). It will do for now.
Un-sprung mass:
For the front I weighed the tires (49 pounds each) and estimated ½ the weight of the MM control arms & springs. I was able to weigh some old rotors and calipers.
Front weight came to ~125 pounds each side or 250 pounds total.
For the rear I used a historical weight of 160 pounds for the axle assembly, added the brakes tires etc. and came to a total of 410 pounds. Regretfully I forgot to check this when the axle was off the car (sigh).
All of this data was entered into a spreadsheet downloaded from Crawlpedia at:
https://www.crawlpedia.com/4_link_suspension.htm
This is a rock crawler website but has a spreadsheet you can download to calculate rear suspension geometry. It is old but it works. The only problem is I have a five-link suspension (the panhard) so the spreadsheet did not calculate the rear roll center height properly.
For a four-link suspension such as the OEM design the spreadsheet calculated the roll center height at about 16”. This is correct. However, with the panhard the roll center is the height of the panhard where it crosses the centerline of the car. In my case this is directly measured off the laser at 6.875”. I simply over-road the formula in that cell (C33 on the VectorCalculations tab) to show the correct value even though the calculation is not used elsewhere.
With all this data entered into the spreadsheet my existing suspension looked like this:
The graphics of the rear suspension are below. Top View is above and Side View below it.
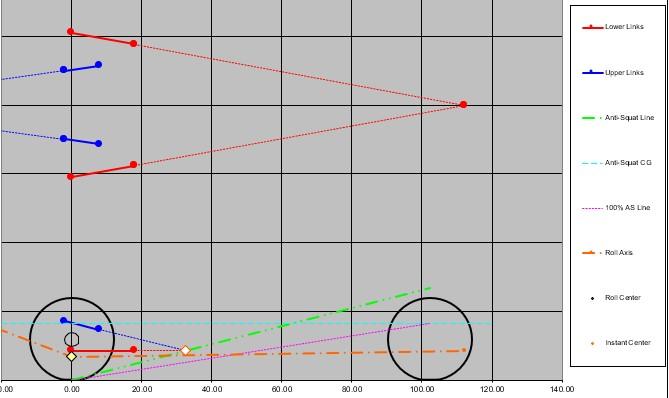
The big surprise was the 162% calculated anti-squat in the center green cell on the top image. That is what you might set up for a drag car.
For reference, the OEM design has an anti-squat of about 60%. The Steeda design probably puts it up around 80% (my guess).
Here is the problem: Anti-squat forces the rear frame of the car UP under acceleration load. Pushing the rear up must push the tires down. As soon as the car starts to accelerate it increases load (more than just weight shift) on the rear tires because it is also raising the rear. Great for drag racing up to a point (too much and you are raising the car instead of pushing it forward - The lift has to balance with the traction).
Great for an angle winder but only up to a lesser point: When you let off the gas and stop accelerating the additional load on the rear tires instantly goes away. This is just as it enters a turn. The unloading of the rear tires can now help cause a spin out. For a Road Track car the books say you should not go above 50%. Or 80%. There is some disagreement.
For an autocross car I suspect these numbers may be conservative. The autocross car is not being set up for long smooth max G cornering. It is constantly in transition. I think a better number to shoot for might be about 100%. But my last name is not Andretti so we will see. I built some adjustment into the final upper link design (more on that later).
Anti-Squat Explained
What is this “anti-squat” you speak of?
Start with the Center of Gravity (CG). It is the balance point of the car in all three dimensions with NO CONSTRAINTS on it. Fling your car into the air (or use a stick). It rotates about a single point while airborne. That point is the CG.
There are less destructive ways of finding the CG but that is for another time and this description helps with the discussion that follows.
We tend to think of our cars as solid objects, but they are not. Think of your car without the wheels and axles “floating” like a boat on its springs (almost like flying through the air).
The car boat rocks in the water fore and aft about its center of gravity (16’ above the water and 42 inches behind the front springs in this case).
If I push the car forward down low from the back in a horizontal line (where the axle would be) you can imagine it tipping up in the front and down in the back as it accelerates (like a normal small boat with an outboard motor). This is because the thrust vector (red dotted line below) is aimed below the CG.
What if I tip that outboard motor so that it is not pushing horizontally? The thrust vector is pushing up at a steep angle as well as forward. If the angle is steep enough (pointed above the CG) the back of my car/boat will raise when it is accelerating (and nosedive into the water and sink. Not recommended. Roll the windows up).
The above is over simplified but not a bad analogy. Your car IS sort of floating on its springs but its rocking motions are “constrained” by suspension linkages connecting it to the ground.
The tires touching the ground are a major constraint, but those forces are “filtered” or “translated” through the suspension linkages and springs (The car is not a solid object).
The actual geometry of how the rear suspension behaves under acceleration is below. This is the same chart from the spreadsheet (above) annotated to show what the anti-squat calculation is doing. Follow through the steps on the right and keep in mind the floating car discussion.
Note that the green diamond showing where the force vector from the rear tires (as filtered through the suspension) intersects the vector pointing up from the front spring is about 160% of the elevation of the CG. So this suspension (as found) jacks up the rear of the car on acceleration. Great for drag racers.
I have gone back and looked at videos of the car from inside and out and I can see it happen but not as pronounced as expected. I suspect that is because I am not running on drag radials on a prepared surface.
I also have had spinouts, on occasion, that seem to be related to lifting the throttle while at max cornering loads… Hmmm…
The new geometry, shown below, looks about the same but is currently set for 65%. I built multiple holes for the upper links into the frame of the car. The next one down will make the anti-squat about 100%. Testing is underway…
The geometry and angles of the links can make a significant difference on how the car behaves. Just a ½” elevation difference in the upper rear links at the frame makes a 40% difference in the anti-squat.
That is why I screwed up the geometry 10 years ago not following the Steeda design more closely.
That is why simply lowering your car can have a profound effect on handling (in a bad way). Lowering changes the angles of the linkages & constraints. You can never change just one thing – other things will change as well.
That is why the upper link towers lean so far back requiring the upper links to be twice as long as they could have been. The longer the links the less the angles change when the car goes over a bump or leans in a corner.
If you have trouble visualizing that: Imagine the upper and lower links were ten feet long and the axle goes over a two-inch bump. The link angles hardly change. Imagine the links were 6 inches long and the same bump. Big geometry change. It is all about the angles.
The above discussion is limited to Anti-Squat. But exactly the same relationships apply to all the suspension dynamics for stopping (anti-dive) and cornering:
Floating car --> Add force vectors/constraints --> instant centers -> New composite force vectors... All filtering the inputs from the ground into the frame of the car.
With some effort most people can wrap their heads around one part of it at a time (like anti-squat). All together this gets wildly complicated (I'm maxed out).
Yet they designed this OEM suspension in the late ‘70s with slide rules, base function calculators, and protractors on drafting tables. That is dammed impressive.
OMG!! I have a headache just reading this. I love the line that this was oversimplified. I'm too simple too understand most of this.
I still think this could be a series of articles for the magazine. Keep us informed how well it works.
Panhard Bar Mod
Ok, as Mustang50 pointed out this crap makes your head hurt. Enough tossing cars in the air and time to cut some steel.
As mentioned earlier, the original cross bracing on the MM panhard would interfere with my upper strut towers if I leaned them back to where I wanted them, Leaning the towers back makes the connecting links longer. The longer the links the smaller the angles change from design when the suspension moves. It is all about angles.
The photo below is the driver side white upper tower leaning back roughly where I want it. The red arrow is pointing at the new panhard bar cross brace. The original location of the brace was where that 5/8” nut is at the top of the white tower. The tower was tilted forward (left) to fit in front of the brace. That made the angle of the linkage (gold) too steep increasing anti-squat and requiring a shorter link.
The photo above has the axle supporting the weight of the car as if it were on the ground.
After buying a length of 1.25” steel tubing from my local steel supply I mocked up where I would thread the new bracing through the car about 3” toward the rear from its original location. Then with the panhard still in the car I cut out the offending pieces.
Here is the removed weldment:
The plan was to connect the new bracing to new frame mounting brackets just behind the originals.
These frame brackets were temporarily mounted to the frame alongside the remaining panhard components. Then I mocked up the new cross brace and tacked everything together. Finally I removed the entire assembly from the car to be welded up and made pretty. My overhead welding is somewhere between horrid and laughable.
You can see in the photo above how this is starting to fit together.
The main structural member transmitting the side loads is the diagonal piece partly missing above. The lower (right side) of it would be the original MM assembly and the upper (left side) of it would be new.
Because this diagonal member sees ALL of the side forces generated by the rear tires (in tension and compression) it needs to be very strong. I reinforced it with a somewhat crudely made inner tube. This was mostly to keep the two parts concentric and give the weld some backing so I could turn up the heat a little.
This was all aligned and clamped for final welding.
The other end of the diagonal brace was then slotted and welded to the new cross brace with a long 3/8” center rib reinforcing both pieces.
This way I did not have to try and taper the two tubes together and it would still be a very strong connection with the rib distributing the loads between the two tubes.
After some clean up and paint (truck bed coating is my favorite) I mounted the new assembly back under the car. The new brackets are bolted to the frame the same as the originals with some tack welds added.
Next is the replacement of the lower control arms with solid rod end links (and then adding back a little urethane). Then new mounting points for the frame end of the upper control arms. That will “complete the thought” on this reconfiguration of the rear suspension. Then we will get to the axle mods.
In the meantime, I am running the car at several events in two SCCA regions. This weekend I will be at a Test & Tune for two days. Still sorting things out.
OMG Please let us know how these updates improved the handling.
Re-Updating the Rear Links
Upper Links
Back on Page 2 of this build log you should find the first major modification to the rear suspension (after the panhard). This arrangement was far superior to the OEM design as it applies to autocross.
But it was flawed in two ways:
Way 1 - The angles between the upper and lower links were not right. I needed to tilt the upper towers back further but did not have clearance to do so. The freshly installed panhard bracing was in the way. This created dragracer levels of antisquat not suitable for autocross. With the car making about 200+ HP it really did not matter at the time.
Way 2 – The upper links were now parallel to the lower links making a proper five link suspension. But the connection points on the frame were still angled at 45 degrees. I had to use double urethane end links (custom from Rod End Supply) to make the connection. It worked well enough but was clunky and had a fair amount of compliance because of the side loads on the bushings.
The photo below is the right side from directly below.
The first flaw (Way 1) was solved in the previous article by relocating the panhard bar bracing toward the rear about 3 inches.
The second flaw (Way 2) was solved by cutting out the old 45 degree mounts and replacing them with new parallel mounts. This was a bit fussy but not really highly technical. You just have to be willing to butcher critical structural suspension mounts on the car with a Sawzall and various other tools of destruction. Not something I was willing to do the first time around. But now…
I used spot rivet drill bits (Amazon) to cut out the spot welds holding the OEM mounting brackets to the car. These bits are fairly inexpensive ($40 for a set). You want the ones that have spring loaded centering points.
Pneumatic chisel and ear plugs also came in handy.
With the bracket removed the underside of the car was exposed and clear for a new mount. That bolt and big washer is for the driver side race harness (left side).
Here are both sides ready to receive new brackets. The gray paint is “weld through” primer.
Test fit of a new 1/8” base plate to mount the new bracket (left side). This would later have a hole bored in it to access that harness bolt.
I made templates from some 1/8” fiberboard after messing around with paper.
The plan was to build some adjustments into these brackets by using multiple mounting holes for the links. That way I could do some testing and determine the best arrangement.
The arc of the mounting holes was determined from a mock up of a link made from a paint stick and marked on the template with the tip of a paint marker. The marking was done with the car supported by the axle and front wheels as if it was sitting normally on the ground.
This was all transferred to steel and then many ½” holes were drilled with half inch spacings on the arc line.
I did this so that, hopefully, I could make adjustment at a T&T and not have to adjust the length of the links to keep pinion angle constant.
This adjustment scheme worked. However, as it turns out only the bottom two holes are useful. The lowest hole is about 80% antisquat. Second from bottom is 105%. The third one is about 140% (drag racer set-up).
For reference the OEM antisquat is 10% or 20% (according to the internet at least) on a stock SN95 car. Perhaps slightly higher on an SVT or Cobra model. Ford would have done this to help minimize drivetrain warranty costs and make the car behave more civilly around the neighborhood. This is routine for most cars. Especially grandma cars.
Mistress came from the factory as a grandma transport vehicle. Believe it or not my grandma drove a brand new red 1969 notchback with a 289 in it. I think it was the first automatic transmission she owned. When someone says they “cant drive stick” my response is that both my grandmothers drove stick most of their lives (after they switched from horses that is). If you have four working limbs you can drive stick! With that said, yes, Mistress is an automatic (sigh).
The two brackets could be welded to the base plate on the bench minimizing welding upside down under the car. I have renewed respect for the steam fitters I used to work with who could make high pressure welds (like 3000 psI) while in awkward positions hanging from staging 100 feet in the air. For me, just making a tolerable weld overhead is dammed hard. Old Curt from the weld shop must be laughing his head off wherever he is {“Just get a flux core wire welder. Any idiot can weld with that! And get a good grinder! You’ll need it!”)
Here are the new brackets in the car.
Stresses on these new brackets are much lower than the original angled mounts because all of the side forces are taken up by the panhard. These only take longitudinal forces. Should be good…
I originally went with solid steel spherical rod ends on both ends of the new links (upper and lower). It was not as harsh as I expected it to be. However, after some test drives and a couple of events I decided that the impulse (shock) loads from rough pavement were too harsh and could cause a failure. One of our autocross sites is pretty darn rough. I replaced one solid rod end of each link with a urethane end link (Rod End Supply). No change in handling and there is now a 95 durometer bit of urethane in each link to take up the shocks.
After two T&Ts and three events the final setting of the upper links was in the second from bottom hole at 105% antisquat. From my books and other research this would be considered out of bounds for a track car. A track car could be more easily upset with throttle adjustments on a long sweeper with this much antisquat.
But as I have said many times, this is no track car. It is an autocrosser. I have noted no issues with upsetting the car in this manner (long fast sweeper under partial power, abrupt lift). Hell, it is always upset. Up to a point I like it upset. Shake that tail! Rotate the car!
At Road America once during a Milwaukee Region Autocross on the small track you could pay $10 during lunch and drive the big 4.2 mile track with speed limited to 60 mph (stewards are watching every move). A couple of takeaways:
So… It is different. Or perhaps I have simply gotten used to throwing my car about the course like a yabo and would get black flagged running at speed. Books and sage advice are the starting point. They don’t necessarily apply to your situation.
The final arrangement shown below looks like this (compared with the similar photo above):
Lower Links
The lower control arms were the last OEM suspension components anywhere on the car. They had never been removed and had the original soft oval bushings. They were worn out and heavy.
As per “Mustang Performance 2 by William Mathis they were also flexible in torsion. He had details on how to reinforce them. He also had details on how to replace them outright with tubular links and rod ends. That is what I chose. Solid spherical rod end on the front and urethane end links at the axle.
As noted, these had never been off the car. They did not come willingly. Three of the four bolts had to be cut out with tools of destruction. Photo below is looking up on the right side.
Lower link geometry is the same as OEM. With the spherical rod end there can be no binding or torsion on the link. The OEM units weigh seven pounds each. The new links weigh 1.5 pounds each (steel tube with SS rod end and CS/urethane end link housing). Total weight savings is eleven pounds. Half of that is un-sprung weight.
By the way, the silver spacers in the photo above are the steel cores from the OEM bushings removed from the front suspension years ago. I have been using them as dies in my press. Cut to length and nickel plated they are perfect for this.
Speaking of spacers: On the axle end of the upper links - I was having difficulty getting the stack up of two spacers and the rod end in position to accept the 5/8” bolt holding it all together. My fingers are too fat, my hands are too inflexible, and it is crowded up there!
Solution: A pair of stiff steel wires bent around the perimeter of the spacer, clamped, and superglued. The wire has to be a little thinner than the spacer.
Now they have handles you can rip off once the assembly is finished.
So with all this Mistress finally had a full-on racing rear suspension. Solid, no binding, adjustable, lightweight, minimal compliance with proper geometry (or at least something like that).
One item of note: It is not as harsh on public roads as one might expect. Very drivable. Or perhaps, I have just gotten used to driving a buckboard around town. I also avoid dirt country roads at all costs.
A friend of mine has a beautiful 2022 BRZ, It is faster than Mistress (just a little). But his son prefers riding in my car at events. The BRZ is smooth, fast, sophisticated, and slick. A marvelous piece of engineering. But Mistress is tactile, rough, loud, visceral, primal, exciting. A proper CAM car I think.
The next part of the write up is adding camber to the rear axle.
So far, with about 120 runs in the book this summer and the last two events yet to come: 1- Things have held together (yea!). 2- After several adjustments to sway bars, tire pressures, axle clamps, and linkages. - I am pretty pleased. I will break it down at the end of season.
The madness continues…
In reply to KentF :
I have really enjoyed reading your analysis of the Mustang drivetrain and suspension. It sounds like you have a fun car and I miss my Mustang GT.
In reply to DrMikeCSI :
Thanks DrMikeCSI. It is fun and I enjoy sharing some of it. Hopefully others find it useful or entertaining or something.
Adding Camber to a Solid Axle
Part 1
Are you really going to do this?
This is radical. Most people don’t do this. Even on a CAM car.
And no one does this to a Ford 7.5 axle. That’s just madness.
This can’t be the only one but there is no record I can find.
If it does not work, I can get a junk axle. But this one is perfectly straight (somehow). The next might not be…
You can just put this back in the car right now. No harm, no foul.
Really going to do this? …
I probably stood there with the portable band saw for ten minutes. Then I started cutting the axle tubes.
When I started autocrossing this car I lamented there was no class for it. There is at least one article in this log lamenting those tribulations. I finally landed in CAM. I knew the car would still not be competitive in a nearly open class against people with nearly open wallets. But I also knew I would have almost as much fun modifying as driving it. And it has been fun indeed. Built it not bought it. The easy stuff is done. So here we go:
These articles do not give a good idea of the actual timeline of reworking the rear suspension and axle geometry. There were a lot of “but first” scenarios that I spent a great deal of time last winter ruminating on:
First, I had to get the car up in the air and suspended on its springs as if it was on perfectly level ground. This included considerations such as tire flex.
Then map the suspension with the LASER, tape measurements, plumb bobs, etc.
Then calculate the antisquat and decide what changes were needed.
Order parts.
Then fab a wooden frame on wheels for the axle and remove it.
But first raise the garage door opener so I could raise the car higher than normal to get the axle out from under it while still on the frame (this was unplanned).
Then, measure fab and install the upper link frame mounts (torque boxes).
Stop all work on suspension and modify the axle (this article).
Reinstall the modified & rebuilt axle and finish the upper links (re-order the RIGHT parts).
Re-support the axle on the frame and block it in position.
Remove the lower links (these were providing consistency of position all this time so I would know to put the modified axle back in the same place).
Order parts.
Replace the lower links.
Re-mount and level the car up in the air and suspended on its springs so I could re-map it and adjust as needed.
The goal of the axle mods was to weld the axle tubes to the diff casting and then cut/reweld them at -1 degree camber.
The axle tubes are pressed into the housing and then plug welded on each side. This is strong enough for normal use. But I am looking to go to fatter tires some day and my usage is anything but normal. I am also contemplating adding external bracing in time.
We are picking up here with making the axle support frame.
The axle frame is an unremarkable construct made from 2x4 and some plywood. Locking steel casters allow movement. Some steel flat stock to hold the axle at the differential welds. It has outer wing supports of wood with some “U” bolts to make sure the axle did not inadvertently fall off. All of the weight is held at the differential. The wing supports are just to keep it from toppling off and to act as a reference. They were also handy for support of the tubes once they were cut. A wood pinion support can be rotated to either side so the axle can be held in nearly any position.
The axle frame and general work area:
The center supports:
I used the LASER level (where have you been all my life?) to verify the axle was level in the frame, straight, and not bent. Somehow, after all these miles and autocross runs it was perfect (winning!).
First order of business was to remove all the internals except the pinion. I have written this up in earlier articles.
Second order was to watch a lot of videos and teach myself how to stick weld. Never did stick. I bought my mutli-process welder last year with this project in mind (this is a year in planning). It can do FCAW, MIG, Stick, & TIG: Omnipro 220 from HF. Nice machine. Still have not tried TIG because it needs straight Argon gas and I am too cheap to buy it until I need it.
I needed to stick weld because you can use nickel rod at lower temperature. Lower temperature means lower risk of cracking the cast steel pumpkin. You can use nickel wire and MIG but that stuff is very expensive and I only need a little. The nickel rod cost about $45. I burned through 2/3 of it practicing.
Stick welding is tricky. You have to touch or scratch the part to start the arc (the power is on all the time) and then pull back instantly. Pull back too far and you break the arc. Amps too low and the rod welds itself to your part. Amps too high and you burn holes in things. You have to control the gap to keep the arc going while depositing material, monitoring and moving the puddle. Oh, and the rod gets shorter every instant.
Again, serious respect for people who do this for a living. That said, with practice and good guidance most people can make a bench weld after a fashion. Making pressure welds hanging from swing staging in the dark? That's magic.
Standard weld prep. All paint and rust removed in the weld area. Used a sanding disk on the Dremel to get down in the crack a bit.
The books say the casting should be preheated to 450 degrees and allowed to cool slowly after welding. I found a propane weed burner worked just fine and I only set fire to the wood frame once.
Crossed my fingers and struck an arc.
With my limited skill I could hold and move the arc about ¾” at a time. I think this was just fine in this case as I skipped around from side to side keeping heat even. Basically, gently tack welding the thing together.
I rotated the axle in the frame as I went so that I was always welding from a good position on the top 1/3.
A few rods and some touch up with the die grinder (not as much as I expected) and the thing looked pretty good.
A recheck with the LASER and it appeared nothing changed (yea). And no cracks!
In the photo above you can see a small horizontal hash mark has been cut into the tube about 2 inches from the casting. That is where the axle will be cut. The hash mark is there to act as a reference to make sure angular alignment is not lost.
The cut will bisect the hash mark and go almost to the bottom of the tube. This will allow the length to be constant while bending the axle up at the cut. It was never cut ALL the way through.
I did however, have to make several cuts in the same kerf since one cut was not wide enough to get the desired angle. I would support the axle by the end to pinch the kerf closed and then cut again removing more material.
This would be difficult to do accurately with a reciprocating saw or cut off wheel. A portable band saw is the right tool for the job.
To know how to set the welder up I inserted a wire with a short bend at the tip into the cut. Then pulled back until the bend caught on the inside. I then marked the outside with a marker. Came out at about 9 gauge thickness (0.15”).
Then I started to MIG weld the joint in similar manner as the stick. A little on this side. A little over there… Let it cool…
Target was 1 degree when cool. After some trial and error I found that about 0.80 degrees was right prior to welding. It would finish up at about 1 degree when cool. All this measured with a basic digital angle finder. I had to re-cut one side because it went too far after cooling. The other way to do this is to use heat alone to create the bend.
By the way, all of the welding was done with the diff cover loosely bolted in place to keep splatter out of it.
Note the C clamp holding the differential down to keep things aligned. There were also carpentry door shims under the wings to keep the angle proper.
In the end, the axle ended up with one degree negative camber on each side. You can see it here against the orange straight edge. It actually looks kind of weird.
Next Part 2. Clean it all out, re-assemble, and see if it binds (it did).
Are you going to be able to autocross this year? I'd really like to see the results of all of your hard work.
In reply to Mustang50 :
Hi Mustang50. I am backlogging these articles. This work was complete last spring and I since have over 120 runs in with two clubs this summer. Been busy and have about six more articles waiting to get written.
It took about half the summer to get the car re-sorted with adjustments to the sway bars, rack, tire pressures, etc. Most of that work was to get rid of understeer.
Also had to remove and re-clean the insides of the axle after two events. No significant signs of wear so I expect (hope) it was leftover cutting and grinding debris. Will take it apart and inspect this winter.
Understeer you say? The car had been well balanced/slightly loose but now had more grip in back than before. The trick was to rebalance it without simply reducing grip at the back (counter productive). I think I was mostly successful.
Mistress is planted. Predictable, balanced and a blast to drive (and slightly loose again).
She works best with an open course where speeds stay over 30 MPH most of the time. At slower speeds the supercharger is not wound up and power becomes a factor. Thinking about some fixes for that...
She is tire limited by the 9" wide wheels. Looking to fix that but $$ is a factor.
Overall- Lateral grip was increased at the rear. This was a success and I would do it again.
Write a book, I'll buy it.
In reply to Mustang50 :
Pre-orders available in the lobby during intermission.
Adding Camber to a Solid Axle
Part 2
With the axle cut and rewelded to my liking I started the job of cleaning out all the metal filings.
First rags on sticks poked through from the ends. Then magnets taped to sticks and poked through.
Each process was followed by a blast of Brake Clean down the tube towards the differential as a wash down.
After several sessions, many rags, and two cans it seemed I was reaching diminishing returns on metal filings. I put the differential back in. The diff had been placed under a rag with its constituent parts organized so it could go back in without messing up the shim packs. I also took caliper readings on the shim packs when they were pulled as protection against a butterfingers moment or a senior moment.
Then the moment of truth: Put the axles in at see if it turns… Nope. Serious binding.
Not surprising. You can put up to -1 degree of camber they say without problems. “They” are typically talking about a Ford 8.8 or 9” with Ford parts inside. Or GM or Mopar parts or whatever. But as I learned long ago, “they” are not talking about my car with my parts the way I am using it. Your mileage may vary.
The problem was the Eaton Tru-Trak. The splined section is near the center of the diff. The splines are about an inch long. The Moser axles are splined for about three inches to fit with a variety different differentials.
The “tunnel” from the differential bearings into the center with the splines is unnecessarily narrow. Some messing around with Prussian Blue and I could see where the sides of the hole was making contact with each axle.
This extra wall thickness in the diff is not doing anything structural. Some of it can be removed and no harm/no foul. Making the axels smaller in diameter would also solve the problem. However, it would also make them weaker.
Weak axles are not a good idea. That is why the OEM axles were replaced with the Mosers years ago.
So how to carve out the axle bore on each side of the differential without filling the helical gears full of debris?
First: No grinding stones. Only carbide bits. Whatever debris is left we don’t need it to be stone or aluminum oxide.
I fashioned a plastic tube by coiling up some sheet plastic and inserting it through the diff. As it tried to uncoil it sealed itself against the inside of the tunnel. Then I connected a shop vacuum to the tube. This would pull most metal filings through the tube instead of letting them fall into the gears. I also covered it with rags and tape and then started cutting with the air grinder.
In the first photo above you can just see the white plastic sheet coiled up inside the diff. The yellow in the second photo is just some cardboard adapting to the shop vac hose. And, Prussian Blue gets on everything.
This worked pretty well:
Grind, flip sides, clean, re-blue, re-assemble, turn by hand, bind a little less, disassemble re-mount in the vice with the vacuum hose, repeat, repeat, repeat.
Probably 10 or more repeats. Lost count. Getting really good at putting the differential together.
Finally, no binding. I took it all apart again and cleaned everything up again. This time I also ran the differential and all internal parts through my HF bucket style part washer. I also sprayed out the axle tubes and wiped everything out as best as possible.
Replaced the end seals also. One had been leaking.
Before final assembly I made a cardboard cover for the diff and painted it all up with black truck bed spray. Hold that thought… There is another story there later. It is just paint, right? What trouble could that possibly cause?
Final assembly did not go without incident; This differential has a little steel puck at the very center the prevents the axles from traveling inboard to the center. If the axles slide too far into the differential the “C” Clips would disengage.
The puck keeps the axles from going too far in and the clips keep them from going out.
During the grinding process I had not been putting the puck in the slot since it was just a test fit. No need for it and it is a tight fit.
It would not go in the slot now. No way.
It took a while but I finally figured out the problem: Looking from the back at the differential the puck fits in a rectangular space. The top and bottom of the space is formed by the machined opening in the diff carriage. But the ends of the space are formed by the flat tips of the axles.
The space is not a rectangle anymore. It is a trapezoid with the top smaller than the bottom. The sides are 2 degrees from each other. Like I said, tight tolerances.
The first photo is the steel puck and a “C” Clip along with the drain plug.
Next is the puck not fitting between the axles.
The fix was to remove the axles, grind the tips down on them a bit, clean them up and reassemble. After a few rounds of this the puck fit where it should.
It’s the little things.
Pre-lubed everything as I assembled since the Brake Clean had removed all traces of lubricant by now.
I actually put some assembly lube on the outer bearings and seals just in case.
I checked the backlash on the gears hoping that all this work did not affect them.
It was right in spec. Apparently; I did not screw up the shims!
Everything was now put together, cleaned out (hopefully), filled with oil, not binding, painted and pretty. I reinstalled the exterior upper link towers and got it all back under the car.
Then I could continue the linkage project.
Next is some more analysis on the results of this madness and why it took almost half the summer to get the car sorted out.
Rear End Mod Results
I gave a preview of this a few weeks ago. The project was a success in many ways.
Part of running an experiment is to change one element and then retest. That is hard to do in real life with limited testing time and budget. All at once I changed the geometry of the rear suspension and contact patch of the rear tires. I also made some minor tweaks to the front camber and bought new tires.
At least the springs and dampers were the same as last season. I figured I would have these changes sorted out in an event or two. But it took about half the summer.
Not that things started out poorly. Mistress was handling just fine at event one. Then again it had been handling just fine last fall also. This is all about nuanced improvements. And I don’t have a team of racing engineers. Just me.
First event was a one-day affair in the freshly paved parking lot of a nearby circle track (Owosso Speedway). The new owner has repaved the track in concrete and paved the large parking area as well. We are running on the concrete parking area. It has sloped sections for drainage which adds "interest" to the course. The new concrete is fiberglass impregnated so it is dusty. It will get much better in time but currently not the best place for sorting out how your car is handling.
It was very hot. We only had about 5 runs and I blew a power steering hose on Run 4. Made a big mess (sorry guys). I had an inkling there was understeer but did not really come away with any concrete conclusions.
The failure was because one of the hoses to the cooler was getting very soft in the heat. This was a custom formed “U” shaped piece that is hard to find. I put much better clamps on it and then reinforced it with SS wire to make sure it did not burst someday.
By the end of the second event I knew the car was in significant understeer compared to the year before. This is good! The back end is holding grip better than the nearly unchanged front. Rear grip has increased by the changes. That was the goal! But I was unsure at the time because it seemed the car was getting squirrely as the weekend wore on.
After the second event I pulled the magnet plugs out of the diff and changed the oil. Lots of metal filings:
The stuff on the plug looks like it might be leftover cutting debris. However, you can see some fine stuff in the drain oil.
Crap… Axle back out of the car and torn down again to see what was happening.
Looking at the splines on the axles I could just detect some wear at the point where the splines in the diff end. Not sure if that was new or was there before. Subtle.
The splines now have to act like 1 degree universal joints. There will always be some friction there due to the misalignment.
On the bearing end of each axle there were new witness marks at each edge of the bearing surface.
The roller bearings are flat and aligned with a slightly new bearing path than before. The axle itself is the inner bearing race.
It’s geometry. The axle is now the hypotenuse of a triangle. That segment is always the longest resulting in a slightly different contact point with the bearing.
Cleaning out with the magnet on a stick showed very fine metal particles that would be from wear rather than from cutting.
So I am getting some internal wear. Is it due to the misalignment of the axles in their splines and new positioning at the bearings? Is it because there was still some coarse cutting debris left circulating around in there?
The gears, however, still looked pristine.
This winter I will tear it down again and only then will we see if all this was just new “break in” wear of if I am going to have to take further action.
The third event was a three-day test & tune at an old airbase. We had a conflict, so I did not arrive until the middle of day two.
Most of that day was spent chasing the squirrel problem which was getting much worse. It seemed the back of the car was randomly trying to go anywhere but straight.
With the whole back of the car in the air some friends and I started searching for something coming loose. Nothing was loose. It all looked great. But Mistress was almost undrivable.
Finally on the next test run I exclaimed to a passenger that I knew exactly what was wrong with the thing. The answer was painfully obvious if you knew how the car was constructed (a troubleshooting advantage I had over the people helping me). But sometimes it takes the neurons time to get in formation. I think I heard a popping sound in my head.
Up in the air again this time lifting with the differential so the weight stayed on the suspension. Pinion angle is all wrong. The axle is held in position by the upper link towers. They were just clamped onto the axle. Always been that way. The axle is rotating in the clamps.
Remember the truck bed spray coating applied to the axle during rebuild? That stuff is polyurethane which is fairly slippery. I can’t clamp it tight enough to keep it from slowly wandering out of position.
As the axle rotated in its mounts the -1 degree camber was turning into +1 degree toe out. That is where the squirrels are hiding!
We eyeballed it and got things roughly lined up again. Torqued it to the point of risking the cap screws. This all to be aligned properly and tack welded when I get home. Problem solved.
By this time, I had also properly identified the understeer. How to fix it without degrading the newfound grip at the rear? Pondering and discussing at dinner…
In the mean time a new problem had cropped up. Right at the end of the day, last runs, the car became very loose. No squirrels, just loose.
First thing in the morning on Day 3 now the front of the car is in the air (jacking rails are great!).
A link had broken on the front sway bar. Luckily I had a spare. While I was under there I set the bar down one notch. This should make the front of the car more compliant, increasing grip slightly.
The photo above shows the link in the middle hole. Moved it to the rear hole (less stiff).
I also lowered front pressure by 2 psi. Back pressure had already been lowered 1 psi based on new inboard/middle/outboard temperature profiles.
This did the trick. I noted also that it was scraping bottom when loading on the trailer. I raised the back end (increased rack) about ½”. This got me back into the desired “ever so slightly loose” range of operation.
So – Late July and I had the car where I wanted it. Now with more grip. Well planted and predictable. Life is good.
Rear grip madness project is a success. The back end is better planted with very tight linkage and lower un-sprung weight. Antisquat is at an acceptable level and no longer seems to upset the car under power.
Three events left to finish the season. Currently 14th in PAX with the Saginaw Valley Region. For me, that is pretty good. We will see if I can find 13th.
You'll need to log in to post.
